Quadratic equations are equations of the form,
An example of a quadratic equation is
Another example is
Quadratic equations can be solved in 3 ways. They are
1. Solution by factorization
2. Solution by completing the square method
3. Solution by the quadratic equation formula.
One thing to note is that before solving any quadratic equation, a test for the availability of factors should be carried out.
For the quadratic equation,
, the test of the availability of factors is given by
When test 1 gives a perfect square, the quadratic equation can be factorized as a product of 2 simple factors. But if test 1 does not give a perfect square, it means the factorization of the given quadratic equation cannot give 2 simple factors.
For instance, in the case of the previous example
The test of the availability of factors = test 1
Where a =1, b=11 and c=28
= 9
9 is a perfect square because 9 is equal to 3 squared that is the square of 3 = 9.
Testing, we have
Now take another equation
, Testing for the availability of factors,we have
Now -7 is not a perfect square, so the factorization of
will not give a perfect square. You can confirm this by working it out.




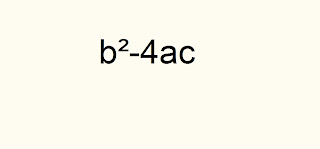







No comments:
Post a Comment